平成30年2月2日(金)講座14『サイエンス教室~身のまわりを科学の目で見る~』の第2回「フォークボール~錯覚の魔球?」を花川北コミュニティセンターで行いました。講師は北海道大学名誉教授でサイエンスアイの千葉忠俊さん、受講者は32名でした。


千葉さんの専門は化学工学で,化学と物理の境界領域で研究することが多く、特に化学プロセスを工業化するときに起こる複雑な現象を一般化してまとめることを得意としてきました。その意味でフォークボールという複雑な現象に取り組む土台があったように思われます。
フォークボールについて考えるようになったきっかけは研究室のコンパで準硬式野球部に所属する学生が「江川の球ってすんごく速いっすよね。浮き上がりますもんね...」と言ったことだったようです。これは本当なのでしょうか?「野茂や佐々木のフォークボールはなかなか打てないよね、ストーンと落ちるものね」とも言われていましたが、これも本当なのでしょうか?また、「...アカシアの雨に打たれてこのまま死んでしまいたい...」という西田佐知子の流行歌がありましたが、雨は2km以上も高い空から降るので打たれて死ぬほど速く落ちて来ることはありません。それはなぜでしょうか?
「フォークボールの落下も雨の落下も、どちらも空気の抵抗の問題として説明できるのでは?」と考え、退職後にパソコンを使って種々計算して得られた結果をまとめたのが今回のお話しですと述べられ、講座が始まりました。


以下に千葉講師のお話の概要を紹介いたします。
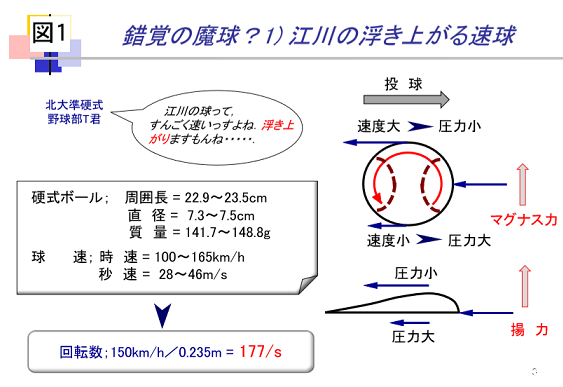
◆錯覚の魔球? (1)江川の浮き上がる速球
ボールが投手からみて下向きに回転しながら空気中を進むとき,ボールの上側を流れる空気速度が大きくなって圧力は小さくなり、反対に下側は速度が小さくなって圧力が大きくなる結果,上向きの力が働きます(図1、右上)。飛行機が浮力を得るときと同じような原理です(図1、右下)。硬式ボールを初速150km/hで投げ.上側の圧力を0にするには、ボールを1秒間に177回転と人間業では到底無理な回転速度を与えなければなりません(図1、左下)。
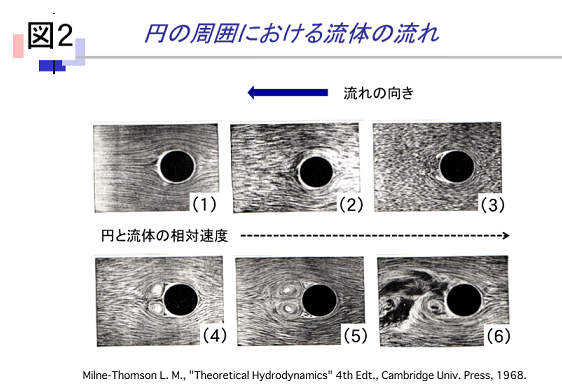
まず、ボール(球)の周りの空気や水の流れを、トイの中の流れに直角に置かれた円柱の周りの流れとして2次元で観察したのが図2です。水の流れが速くなると,円の後ろ側で"渦"ができます(図2、(3))。流れが速くなると,2個の渦がはっきり現れ(図2、(4))、さらに流れが速くなると渦が水に引っ張られて円から離れます(図2、(5)と(6))。流れが速い場合には,このような渦の生成と剥離が不規則に繰り返されます。
◆雨に打たれて死にたい?
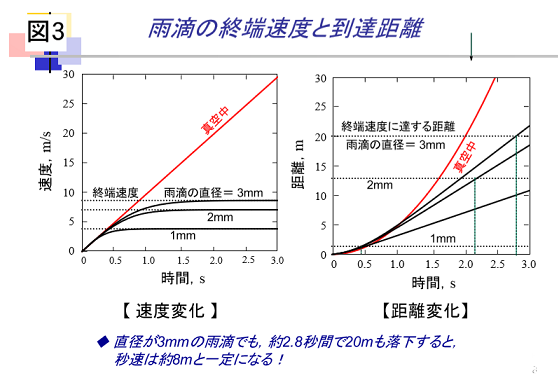
球が落下する場合、真空中では球に働く力は[重力]だけで、これにより落下を続ける[運動力(慣性力)]が得られます。これに対し,空気中落下する場合は[重力]の他に[浮力]と[抗力(粘性力)]が上向きに働き、その結果として[慣性力]が得られるので、落下中に[重力]と([浮力]+[抗力])が同じになると、[慣性力]がゼロとなって球は一定速度(終端速度)で落下します。雨滴を球形として、雨滴が落下を始めてからの落下速度と落下距離の変化は図3ようになります。真空中では落下速度は時間に比例して大きくなるが、空気中では浮力と抗力が働くため一定速度(終端速度)に落ち着きます。直径3mmの雨滴の場合、終端速度は約8m/sで、約2.8秒間で20mも落下すると秒速8m/sの一定速度になることがわかります。この程度の速度で雨に打たれても死ぬようなことはないでしょう。
◆錯覚の魔球? (2)フォークボール
硬式野球ボールについて、「フォークボールは二次元無回転運動」と「球場(ドーム球場など)内は無風状態」という仮定をしたときの水平および垂直方向の運動方程式は
水平方向: [慣性力]= ―[抵抗力]
垂直方向: [慣性力]=[重力]―[浮力]―[抵抗力]
と書かれるので、これらの式に基づいて水平方向の初速度が120~165km/hのボールの運動を数値解析しました。まず、縦軸に地上からの高さ(m)、横軸に投手から捕手への水平方向距離(m)をとった"ボールの軌跡"をみても、ボールがストーンと落ちるような変化は現れませんでした。そこで、まず、ボールの初速が140km/hの場合で、縦軸に地面からの高さ(m)、横軸に時間(s)をとってボールの落下曲線を描いてみると,空気中でも真空中の自由落下とほぼ同じ曲線となりました。
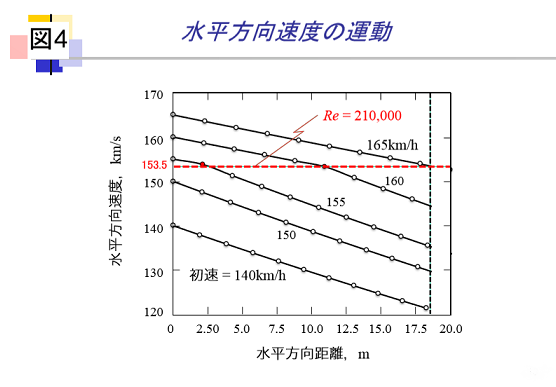
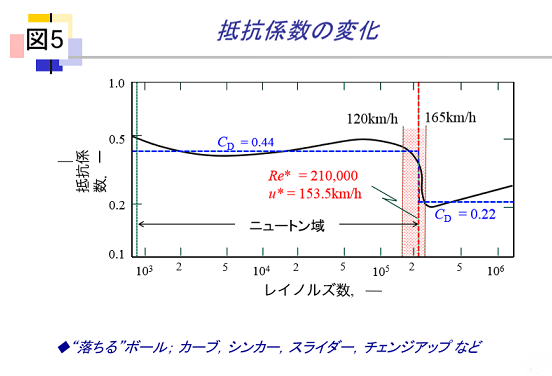
つぎに、水平方向の運動に着目してボールの速度(km/h)の変化をみると、図4のようになります。図から、初速が155km/hと160km/hのボールが投球板から2.50mおよび11.7mに達したときに速度が急減することがわかります。この急減が起こる速度は153.5km/hで、[慣性力]と[粘性力]の比であるレイノルズ数(Re)が210,000の場合に対応します。これは、ボールが投げられてから抵抗係数が階段状に増加する流れの領域(帯状の影の部分)を通過することによるもので、これによりボールが"ストーン"と落ちる原因と思われ(図5)、ボール後流で起こる渦(図2、(6))の剥離と関連するフォークボールの正体と思われます。
いずれにしても、フォークボールは水平方向に進む速度が急減するボールで、打者は"ストーンと落ちる"と錯覚するボールと云えそうです。
◆錯覚の魔球? (3)サッカーボール
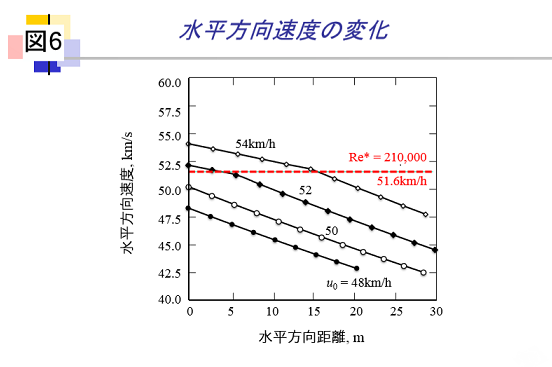
サッカーボールの運動も硬式野球ボールの場合と同じように、二次元無回転運動と無風状態の球場内という仮定を用い、ペナルティーキック(距離;10.97m)を想定して数値解析しました。この場合はレイノルズ数(Re)が210,000となる水平方向初速度は51.6km/hであり、野球の硬式球の3分の1程度となります。サッカーボールの水平方向速度(km/h)と水平方向距離(m)の関係は図6のようになり、水平方向速度は51.6km/h(レイノルズ数(Re)が210,000)になると、急減することがわかります。
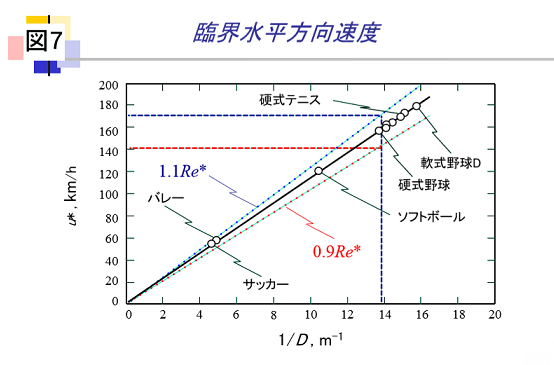
硬式野球やサッカーボール以外の様々な球技のボールについてレイノルズ数(Re)が210,000となる水平方向初速度は図7のようになります。速度の急減が起こる臨界速度は球の直径D(m)の逆数(1/D)に比例することがわかります。
余談になりますが、硬式ボールの運動の解析から、プロ野球投手が高度の技術を有していることがわかりました。計算結果によると、初速140km/hの投球でストライクを取るには、仰角の幅はわずか0.5~2.5度です。また、初速160km/hの場合は幅がー0.5~2.0度となります。これを繰り返し実践するには並々ならぬ能力と鍛錬が必要なはずであり、改めてプロの技術の高さに驚かされます。
時間的な余裕があったので、7人の受講者から質問や要望を出していただき、それぞれに対し千葉講師から丁寧で的確な説明をしていただきました。例えば、「抵抗係数の説明を再度して欲しい」、「フォークボールは球の重さによって変わらないのか?」「流体の速度を早めると渦ができ、その渦が離れて行くとあったが、投手自身は球がどこに飛んで行くのかわからないのか?」などの質問がありました。
今回は身近にある野球やサッカーについて千葉講師からインパクトのあるお話を聞くことができました。
受講者の感想や意見として以下のようなものがありました。
・知の追求はとても楽しく、目からウロコで、今後もサイエンスは興味ある分野です。
・文化系で物事を見ていた中で物理学を通じて数式を使って考えることが少ないため刺激的に聴講させていただきました。運動や行動を数値化する思考の重要性も改めて考えさせられました。
・野球という話題をもとに多くの身のまわりの科学を感じることができました。科学の未知さ、難しさを知りました。
・野球投手の技術と能力、体力等の大変さを知りました。
・飛行機の浮力について覚えている内容と違ってオドロキました。
・難しかったです。自分には無理かなと思われる講座も「参加」すると何かしらの知識に接することができ、とても有り難いです。質問の時間、良かったですね。
・面白そうだが理解するのに時間がかかりそう!










